中学受験、計算の暗記は必要か？

九九だけではなく、「１□×１△」の２桁のかけ算（※）まで暗記させようとするひとたちがいるようです。

※例：１６×１９

暗記なんてしなくてもほんの少し訓練すれば、２、３秒で（※）暗算できるようになりますけどね。
※加齢でボケてきたおっさんの話。若い子だとパッと見ただけで答えがでるのではないでしょうか。

実際、小２でも１か月もかからないうちに高速で暗算できるようになりましたしね！

それに、暗記だと記憶があいまいになればミスするので定期的にメンテする必要がでてきます。

暗記に頼ると――。
・人間、誰しも忘れる　→　何度も覚えなおさないといけない。塵も積もれば、で勉強時間が増える
・ほかに覚えることがたくさんある　→　メンテだけで勉強時間がかなりとられる。勉強時間が増える

つまり、計算まで暗記させると、そういうことが積み重なって子どもにめちゃくちゃ勉強させることになるわけですな。

…うちの子どもたちが、すぐに高速で暗算できるようになったのは、地頭？（センスともいう）

いやいや、
この程度のことで地頭はないでしょ。
そういうものが必要とされるのは灘の算数のレベルではないでしょうか。

何でもかんでも子どもの能力に責任転嫁すんなよ、と思います。

ちなみに、子どもたちが速攻で習得したのは、「計算ばかり」みたいな愚かなことをせずに、先に算数の思考力をあげたためです。指導次第なのに何でもかんでも地頭のせいにされて、子どもが可哀そうです。  

具体的にどのように教えればいいのか？

ザっと、ですが、以下。

ちなみに、図は以下のような感じです。この形にこだわらず、子どもが理解しやすい、暗算しやすい形にすればいいですよ！　というより、お子さんに試行錯誤させて暗算しやすい形を自分で作らせるといいのではないでしょうか。

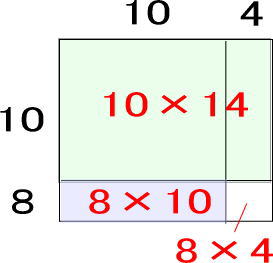
ただ――。

３．１４のかけ算のように暗記すれば便利なものもあるかもしれませんが、四谷大塚の偏差値６０前半までは計算の暗記は一切必要ないことは確認しました。

暗算も不要、ひっ算で十分です。

それで試験の時間が足りないというのであれば、別のところに問題があると思います。

が、男子御三家以降だと話は別かもしれないので、その辺がわかればまた記事にしようと思っています。
もっとも、灘の算数を見据えて暗算の訓練をするようになったので、３桁のかけ算の暗算が芳しくなければ暗記させるかもしれませんけどね。でもまあ、息子はあと２年以上あるので、間に合うと思いますが。

少し話は変わりますが、「通塾する前に計算問題をやっとくんだった！」という記事を見かけます。

（どのレベルを目指すのかによりますが）別のところに問題があると思いますけどね。

↓さまざまな受験のブログを読めます。

にほんブログ村

・中学受験に関する情報は、中学受験から攻略にもまとめています。